Union-Find Algorithm, Quick-Union
Union-Find Algorithm, Quick-Find 1. 정의 * Union Command, 두 오브젝트를 연결하는 것 * find query, 두 오브젝트가 연결되어있는지 확인하는 것 2. 용도 그림과 같이 A 노드와 B 노드가 있다고 해봅시다. A와 B가
songye.tistory.com
Union-Find Algorithm, Quick-Find
1. 정의 * Union Command, 두 오브젝트를 연결하는 것 * find query, 두 오브젝트가 연결되어있는지 확인하는 것 2. 용도 그림과 같이 A 노드와 B 노드가 있다고 해봅시다. A와 B가 연결되어 있는지 확인하
songye.tistory.com
두 포스팅을 보거나 꼭 Quick-Union or Find를 알고 오는 것을 추천합니다.
자 지난시간에 Quick-Union에 대해 배웠습니다.
Quick-Union의 치명적인 단점은 Tree의 깊이가 깊어질수록 (최악의 경우)
find, unite 둘다 O(N)의 시간이 걸렸습니다.
하지만 만약 Tree를 Flat하게 만들 수 있다면? Root를 탐색할 때 오래걸리지 않을 겁니다. O(N)만큼 걸리지는 않겠지
자 그럼 한 번 알아봅시다.
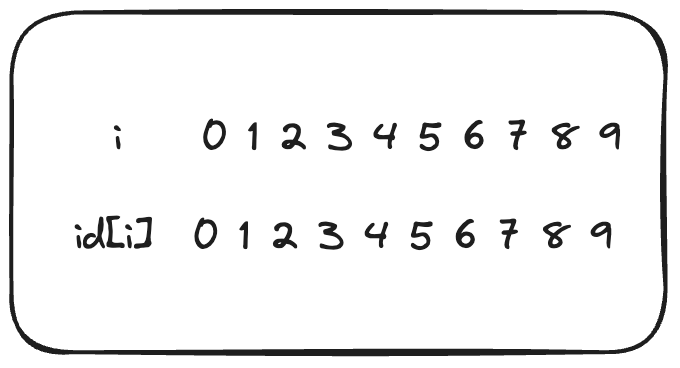
자 다음과 같은 id Array가 있다고 해봅시다. (또또 써먹네 이거)


그림 1-2 와 1-3와 같이 unite된 경우가 있따고 가정해보면
1. Quick-Union
Quick-Union의 경우 unite(3,5)를 할 경우에
5번 노드의 루트 밑으로 무조건 3번 노드의 루트 노드가 병합됩니다. (기억나시나요?)
2. Weighted Quick-Union
여기서 장치 하나를 추가합니다.
Size라는 Array 변수를 하나 만들고 각 집합의 사이즈의 값이 들어가도록 합니다.
그리고 unite를 할 때 두 노드가 속한 집합의 크기를 비교하여
작은 집단이 큰 집단으로 들어가도록 설계한 알고리즘이
바로 Weighted Quick-Union입니다. (강약약강)
그림 1-3 같은 경우에는 6번 노드가 9번 노드 바로 밑으로 들어가겠죠

아늬 이렇게 사이즈 비교해도 완전 플랫하지는 않은데요?
순차적으로 큰 집합끼리 형성되고 걔네들끼리 합쳐지면 어떡할껀데요?

3. Path Compression
이 깊어진 트리를 더 Flat하게 만들어줄 장치가 또 하나 있는데
바로 path compression입니다.
이게 뭐냐 그림으로 보면 이해하기 쉽습니다.
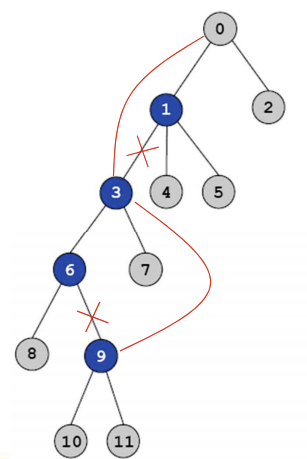
자 9번 노드를 기준으로 보면 root 명령어를 받으면 root를 탐색하기 위해
지나가며 방문하게되는 노드들이 있습니다
1, 3, 6번을 지나가게 되는데요 이 1,3,6 노드들을
루트 노드 아래에다가 놓으면 Flat한 Tree가 완성되지 않을까요?

4. Code
(1) weightedQuickUnion
public class WeightedQuickUnion {
private int[] id;
private int[] sz;
public WeightedQuickUnion(int N) {
id = new int[N];
sz = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
sz[i] = 1;
}
}
public int root(int i) {
while (id[i] != i) {
i = id[i];
}
return i;
}
public boolean find(int p, int q) {
return root(p) == root(q);
}
public void unite(int p, int q) {
int rootP = root(p);
int rootQ = root(q);
if (sz[rootP] > sz[rootQ]) {
id[rootQ] = rootP;
sz[rootP] += sz[rootQ];
}
else {
id[rootQ] = rootP;
sz[rootQ] += sz[rootP];
}
}
}
자 여기서 path Compression을 추가하고 싶다면 root 부분에
public int root(int i) {
while (id[i] != i) {
id[i] = id[id[i]];
i = id[i];
}
return i;
}
id[i] = id[id[i]];
이 한 줄을 추가하게 되면 할아버지 노드 밑으로 들어가게 됩니다.

빨간줄을 잘보면 9번이 3번 밑으로 3번이 0번 노드 밑으로 들어가는 것처럼 말이죠
어? 그러면 왜 모든 노드들을 0번 노드 밑으로 안하나요?
여기서 필자의 생각은 root 탐색이 빈도가 높기 때문이라고 생각합니다.
아버지 노드 밑으로 들어가던 할아버지 노드 밑으로 들어가던 root가 엄청 많이 반복되면
더 적은 횟수로 Flat해지기 때문에 그렇지 않나 싶습니다
5. 결론
Weighted-Quick-Union 은 Quick-Union에 사이즈라는 변수를 추가해
크기를 비교한 후 Flat한 Tree를 만드는 것이다.
Path Compression은 더 평평하게 만들어 주는 좋은 장치!
자 시간 복잡도 표를 보며 Union-Find Algorithms은 여기서 마무리 하겠습니다.
증명은 어려우니 넘어갈게요,, 못합니다,,

union-find 알고리즘을 마무리하며
다음 프로젝트로 union-find 알고리즘과 관련된
GO, HEX 게임 같은 걸 만들어보면 어떠려나 생각중입니다,,
생각만,,

'Computer Science > Data Structure & Algorithms' 카테고리의 다른 글
| Data Structure, Generic Stack & Queue (1) | 2024.02.29 |
|---|---|
| Data Structure, Queue (0) | 2024.02.28 |
| Data Structure, Stack (1) | 2024.02.27 |
| Union-Find Algorithm, Quick-Union (0) | 2024.02.22 |
| Union-Find Algorithm, Quick-Find (0) | 2024.02.22 |



